Dr. Piers Lawrence
Profile
I am passionate about the development and application of novel mathematical and algorithmic solutions to real-world problems. My research projects in the past have explored diabetes care, measuring chaotic pendulum systems, evaluating special functions, finding periodic points in fractal sets, and designing stable algorithms for the solution of polynomial eigenvalue problems.
Currently, I am working as a mathematical consultant at EigenPoly Consulting, where I am working with a diverse range of industrial firms to help bring their products to market. I specialize in providing expert mathematical advice and novel algorithmic solutions to a diverse range of optimization and computational problems.
I obtained my PhD from The University of Western Ontario, in London, Canada, under the supervision of Rob Corless. During my PhD studies, I developed methods for the stable computation of the roots of polynomial equations expressed in Hermite and Lagrange bases and for barycentric rational interpolants, as well as exploring structured condition numbers and structured backward error for companion matrices.
From 2013 to 2017, I was a postdoctoral researcher hosted within Department of Computer Science at the KU Leuven, Belgium, where I continue to have active collaborations with members of the Numerical Integration, Nonlinear Equations & Software (NINES), the Numerical Approximation and Linear Algebra Group (NALAG), and the DistriNet groups. My research has focused on a number of different areas, including the development of new linearizations of matrix polynomials and the analysis of their backward errors, as well as investigating the robust identification of insulin pump parameters for diabetic patients.
Most recently, I led an award-winning applied research project in Kikwit, DR Congo, where we developed networked embedded systems for the remote monitoring of the medical cold chain for blood, vaccine, and medication storage at local health facilities.
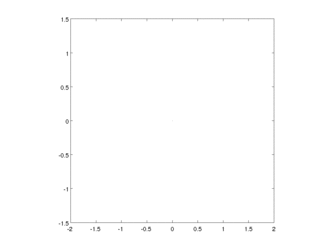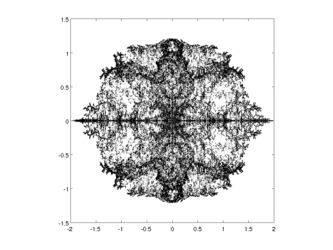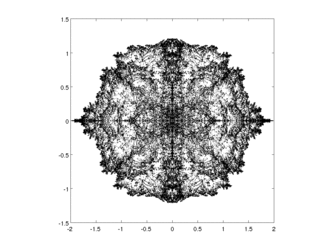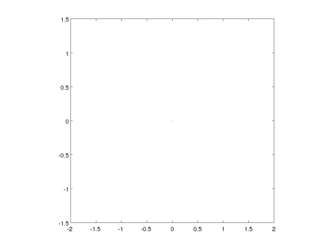
Animation of the 21-periodic points under iteration of the Mandelbrot map (See Mandelbrot)
